Лекция: Лекции по матану (III семестр) переходящие в шпоры
№1
1 Двойной интеграл
Рассмотрим в плоскости Оху замкнутую область D, ограниченную линией Г,
являющейся замкнутой непрерывной кривой. z = l(P) = f(x,y), P= (x,y) Î D
– произвольные ф-ции определенные и ограниченные на D. Диаметром области D наз.
наибольшее расстояние между граничными точками. Область D разбивается на n
частых областей D1.Dn конечным числом произв. кривых. Если S – площадь D, то
DSi – площадь каждой частной области. Наибольший из диаметров областей обозн l.
В каждой частной области Di возьмем произв. точку Pi (xi , Di) Î Di, наз.
промежуточной. Если диаметр разбиения D l à 0 , то число n областей Di
à ¥. Вычислим зн-ие ф-ции в промежуточных точках и составим сумму:I
= 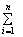 f(xi, Di)DSi (1), f(xi, Di)DSi (1),
наз. интегральной суммой ф-ции. Ф-ция f(x,y) наз. интегрируемой в области D
если существует конечный предел интегральной суммы.
Двойным интегралом ф-ии f(x,y) по области D наз. предел интегральной суммы при l
à 0. Обозн:
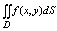 или или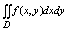
2 Понятие числового
ряда и его суммы
Пусть задана бесконечная последовательность чисел u1, u2, u3.
Выражение u1+ u2+ u3.+ un (1) называется числовым рядом, а числа его
составляющие- членами ряда.
Сумма конечно числа n первых членов ряда называется n-ной частичной суммой
ряда: Sn = u1+..+un
Если сущ. конечный предел: 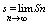
, то его называют суммой ряда и говорят, что ряд сходится, если такого предела
не существует, то говорят что ряд расходится и суммы не имеет.
№ 2
1 Условие существования
двойного интеграла
Необходимое, но недостаточное:
Ф-ция f(x,y) интегрируема на замкнутой области D, ограничена на D.
1 достаточный признак существования: если ф-ция f(x,y) непрерывна на
замкнутой, огр. области D, то она интегрируема на D.
2 достаточный признак существования: если ф-ция f(x,y) ограничена в замкнутой
области D с какой-то границей и непрерывна в ней за исключением отдельных
точек и гладки=х прямых в конечном числе где она может иметь разрыв, то она
интегрируема на D.
2 Геометрический и арифметический ряды
Ряд состоящий из членов бесконечной геометрической прогрессии наз.
геометрическим: 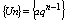
или
а+ а×q +.+a×qn-1
a ¹ 0 первый член q – знаменатель. Сумма ряда: 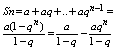
следовательно конечный предел последовательности частных сумм ряда зависит от
величины q
Возможны случаи:
1 |q|<1 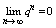
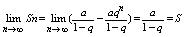 т. е. ряд схд-ся и его сумма т. е. ряд схд-ся и его сумма 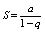 2 |q|>1 2 |q|>1 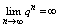 и предел суммы так же равен бесконечности и предел суммы так же равен бесконечности
т. е. ряд расходится.
3 при q = 1 получается ряд: а+а+.+а. Sn = n×a 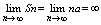 ряд расходится ряд расходится
4 при q¹1 ряд имеет вид: а-а+а . (-1)n-1a Sn=0 при n
четном, Sn=a при n нечетном предела частных суммы не существует. ряд
расходится.
Рассмотрим ряд из бесконечных членов арифметической прогрессии: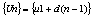
u – первый член, d – разность. Сумма ряда 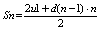
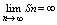 при любых u1 и d одновременно ¹ 0 и ряд всегда расходится. при любых u1 и d одновременно ¹ 0 и ряд всегда расходится.
№3
1 Основные св-ва 2ного интеграла
1. Двойной интеграл по области D = площади этой области.
2. Если область G содержится в Д, а ф-ция ограничена и интегрируема в Д, то
она интегрируема и в G.
3. Аддитивное св-во. Если область Д при помощи кривой г разбивают на 2 области
Д1 и Д2, не имеющих общих внутренних точек, то: 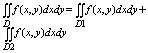
4. константы выносятся за знак интеграла, а сумму в ф-ции можно представить в
виде суммы интегралов:
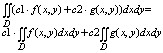
5. Если ф-ции f и g интегрируемы в Д, то их произведение также интегрируемо в
Д. Если g(x,y) ¹ 0 то и f/g интегрируема в Д.
6. Если f(x,y) и g(x,y) интегрируемы в Д и всюду в этой области f(x,y) <=
g(x,y), то:
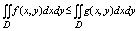
В частности: g(x,y) >=0 то и
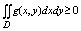
7. Оценка абсолютной величины интеграла: если f(x,y) интегрируема в Д, то и
|f(x,y)| интегрир. в Д причем
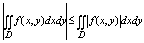
обратное утверждение неверно, итз интегрируемости |f| не следует
интегрируемость f.
8. Теорема о среднем значении.
Если ф-ция f(x,y) интегр. в Д., то в этой области найдется такая точка (x, h)
Î Д, что:
 (2), где S – площадь (2), где S – площадь
фигуры Д. Значение f(x, h) опред по ф-ле (2) наз. средним значением ф-ции f по
области Д.
2 С-ва сходящихся рядов
Пусть даны два ряда: u1+u2+.un =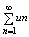 (1) и v1+v2+.vn = (1) и v1+v2+.vn = 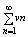 (2) (2)
Произведением ряда (1) на число l Î R наз ряд: lu1+lu2+.lun =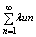 (3) (3)
Суммой рядов (1) и (2) наз ряд:
(u1+v1)+(u2+v2)+.(un+vn) = 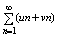 (для разности там только - появица) (для разности там только - появица)
Т1 Об общем множителе
Если ряд (1) сходится и его сумма = S, то для любого числа l ряд 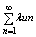
=l ×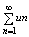 тоже тоже
сходится и его сумма S’ = S×l Если ряд (1) расходится и l ¹ 0, то и
ряд 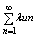 тоже тоже
расходится. Т. е. общий множитель не влияет на расходимости ряда.
Т2 Если ряды (1) и (2) сходятся, а их суммы = соотв S и S’, то и ряд: 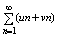
тоже сходится и если s его сумма, то s = S+S’. Т. е. сходящиеся ряды можно
почленно складывать и вычитать. Если ряд (1) сходится, а ряд (2) расходится, то
их сумма(или разность) тоже расходится. А вот если оба ряда расходятся. то
ихняя сумма (или разность)может как расходится (если un=vn) так и сходиться
(если un=¹vn)
Для ряда (1) ряд 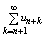
называется n – ным остатком ряда. Если нный остаток ряда сходится, то его сумму
будем обозначать: rn = 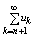
Т3 Если ряд сходится, то и любой его остаток сходится, если какой либо остаток
ряда сходится, то сходится и сам ряд. Причем полная сумма = частичная сумма
ряда Sn + rn
Изменение, а также отбрасывание или добавление конечного числа членов не
влияет на сходимость (расходимость) ряда.
№4
1 Сведение
2ного интеграла к повторному
Пусть у1(х), у2(х) непрерывны на отрезке [a, b], у1(х)<= у2(х) на всем отрезке.
D={x,y}: a<=x<=b; y1(x)<=y<=y2(x)
Отрезок [a,b] – проекция Д на ось ох. Для такой области людбая прямая,
параллельная оу и проходящая через внутреннюю точку области Д пересекает
границу области не более чем в 2 точках. Такая область наз. правильной в
направлении оси оу.
Если фция f(x,y) задана на Д и при каждом х Î [a,b] непрерывна на у , на
отрезке, [y1(x),y2(x)], то фц-ия F(x) = 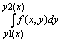
, наз. интегралом, зависящим от параметра I, а интеграл : 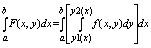
, наз повторным интегралом от ф-ции f(x,y) на области Д. Итак, повторный
интеграл вычисляется путем последовательного вычисления обычных определенных
интегралов сначала по одной., а затем по другой переменной.
2 Необходимый
признак сходимости рядов
Если ряд сходится, то предел его общего члена равен нулю: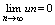
Док-во: 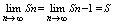
Страницы: 1, 2, 3, 4, 5, 6
| 


