|
Д(Z)- дисперсия Д((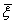 - - 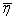 )/s( )/s(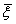 - - )) = )) = 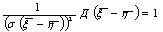
M(Z) = 0; Д(Z) = 1. Для того, чтобы выбрать Zкр. и при заданном уровне
значимости a, определить принимается или не принимается основная гипотеза,
найти вероятности.
P(0 < Z < Zкр.) + P(Z > Zкр. прав.) = ½ Ф(Zкр.) + a/2 = ½
Ф(Zкр. прав.) = ½ - a/2
Zнабл. = 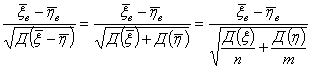
|Zнабл.| < Zкр.прав. Þ Н0 |Zнабл.| > Zкр.прав. Þ Н0 отвергается.
38. Проверка гипотезы о равенстве генеральных средних при неизвестных
дисперсиях.
Пусть x и h нормально распределенные СВ, предполагается, что неизвестны, но
равны между собой дисперсии. x1, x2, ... , xn h1, h2, ... , hm
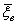 ; ; 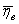 : Н0: М(x) = М(h) Н1: М(x) ¹ М(h) : Н0: М(x) = М(h) Н1: М(x) ¹ М(h)
Для проверки гипотезы Н0, вводится СВ t, которая представляет собой
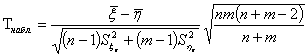
Теоретическое обозначение признака; СВ Т распределена по закону Стъюдента,
зависит от первого параметра, который называется числом степеней свободы (k).
k = n + m – 2 (по таблице для распределения Стъюдента при заданном значении k
и уровне значимости a в зависимости от вида альтернативной и конкурирующей
гипотезы, находятся либо односторонние tкр., либо двухсторонние tкр.).
Ткр. прав. = - Ткр. лев. | Тнабл. | < Ткр. двуст. Þ Н0 | Тнабл. | >
Ткр. двуст. Þ Н0 отвергается.
42. Марковские случайные процессы. Размеченный граф состояний.
Предположим, что дана система S. Предп., что состояние этой сис-мы хар-ся
параметрами состояний. Если состояние системы меняется во времени случайно, то
говорят, что в сис-ме протекает случайный процесс. Сис-ма —аудитория. Для
хар-ки состояния используется параметр—число студентов, тогда эта система с
дискретными состояниями. Будем рассматривать системы с дискретными состояниями
и непрерывным t: сис-ма мгновенно в произвольные сегменты t скачками меняет
состояние. Если параметр t принимает дискретные значения (t=1,2,3,...), то
происходит процесс с дискретным временем (случайная последовательность), если
же t изменяется на некотором интервале, то процесс с непрерывным временем. Если
случайные величины семейства принимают дискретные значения, то имеет место
процесс с дискретными значениями, если же непрерывное, то с непрерывными
значениями. Предположим, что рассматривается система с дискретными состояниями
и непрерывным t. Пусть S1, S2,...,Sn —возможные состояния сис-мы. Для описания
процесса, происх. в сис-ме, надо знать вер-ти каждого состояния на произвольный
момент t. Р1(t)—вер-ть того, что в момент t сис-ма находится в 1-ом состоянии.
Процесс, протекающий в системе, наз. марковским, если для него вероятность
попасть в состояние Xi=Si в момент ti зависит не от всего прошлого, а лишь от
состояния Xi-1=Si, в котором процесс был в предыдущий момент времени ti-1.
Графом называется совокупность вершин и дуг, соединяющих эти вершины. Для
описания процесса, протекающего в системе, удобно использовать размеченный граф
состояний, в котором в кач-ве вершин исп-ся различные состояния системы, а в
кач-ве дуг—стрелки, показ. возможные переходы за 1 шаг из состояния в
состояние. При этом над каждой стрелкой указ. Плотность вероятности
соответствующего перехода.
43. Система дифф. уравнений Колмогорова для вероятностей состояний.
Пусть дан марковский случайный процесс. Рi(t)—вер-ти состояний: i=1,n(все с
чертой), тогда для Рi(t) выполняется следующее дифференциальное уравнение
d Рi(t)/dt=å( от i<>k,k=1 до n) lki* Рi(t)—å( от
j<>1,j=i до n) lij*Pi(t); i=1,n(все с чертой) (1) Система из n уравнений
, т.к. для любого момента t å( от i=1 до n) Pi(t), то в системе (1) одно
любое уравнение м-но отбросить. И, задав начальное условие на момент t=t0,
P1(t0)=1, Pi(t0)=0, i=1,n( все с чертой).
В итоге м-но решить сис-му дифф. ур-ний и найти все вер-ти состояний Pi(t),
i=1,n(все с чертой).
44. Предельные вероятности состояний. Нахождение предельных вероятностей.
Предположим, что дан марковский случайный процесс, тогда, используя уравнение
Колмогорова, можно найти Рi(t); i = 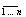
Предельными или финальными вероятностями называют пределы
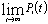 , если эти вероятности существуют, т.е. , если эти вероятности существуют, т.е. 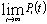 = Рi. = Рi.
Если эти предельные вероятности существуют, то в системе устанавливается
стационарный режим, при котором состояние системы меняется случайным образом,
но вероятность каждого состояния остается неизменной.
Предельная вероятность в марковском случайном процессе существует, если этот
процесс удовлетворяет свойству транзитивности. Процесс в протекающей
системе называется транзитивным, если существует интервал времени t
, в течение которого система может перейти из любого состояния Si в любое другое
состояние Sj.
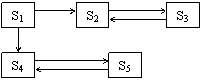 Алгебраические уравнения для предельной вероятности состояний Алгебраические уравнения для предельной вероятности состояний
Пусть марковский случайный процесс удовлетворяет свойству транзитивности, тогда
для него при t ® ¥ существуют предельные вероятности состояний Pi=const.
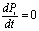 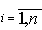
, Þ, в этом случае вместо дифференциального уравнения Колмогорова
получили систему линейных уравнений относительно вероятности состояний
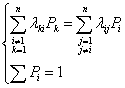
Одно уравнение отбрасывается, остается n уравнений, решая эту систему
получаем Р1, Р2, ... , Рn.
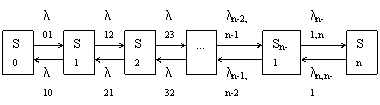
45. Процессы гибели и размножения. Формулы для нахождения предельных
вероятностей.
 Мы предполагаем, что все Мы предполагаем, что все
потоки, переводящие систему из любого Si в Si+1 и из Si в Si-1 являются
простейшими.
li, i+1
li, i-1
Процессы такого типа называются процессами гибели и размножения.
Составим систему уравнений для нахождения предельной вероятности состояний:
S0: l01P0 = l10P1 S1: l10P1 + l12P1 = l01P0 + l21P2 S2: l21P2 + l23P2 =
l12P1 + l32P3 ... Sn: ln, n-1 Pn = ln-1, n Pn-1 P0 + P1 + P2 + ... + Pn = 1
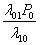 Из первого уравнения выражаем P1 = Из первого уравнения выражаем P1 =
l01P0 + l12P1 = l01P0 + l21P2
P2 = 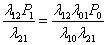
P3 = 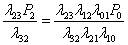 Pn = Pn = 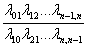 ... ...
P0 + 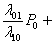 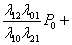 ... + ... + 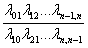 = 1 = 1
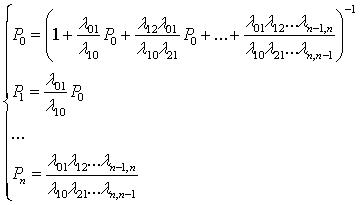
46. Потоки событий. Простейший поток и его свойства.
 Потоком событий называется Потоком событий называется
последовательность каких-то однородных событий, следующих друг за другом через
случайные интервалы времени, т.е. в произвольные моменты времени.
Потоки избираются на числовой оси, представляющей ось времени, точками,
соответствующими моменту наступления событий.
Например: - поток вызовов, поступающих на станцию скорой помощи;
- поток автомобилей, пересекающих перекресток.
Среднее число событий, происходящих в единицу времени называется
интенсивностью потока. l - среднее число событий в потоке, происходящее за
единицу времени. Свойства потока:
1. 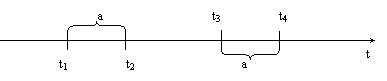
Поток называется стационарным, если вероятность наступления того или иного
числа событий за интервал времени длины а зависит от длины этого интервала и не
зависит от того, в какой момент времени начинается отсчет этого интервала.
t2 – t1 = a
2.
Поток событий называется потоком без последействия (без последствия), если
для любых непересекающихся интервалов времени длины t1 и t
2.
Вероятность появления того или иного числа событий в интервале t2 не зависит
от того, какое число событий произошло в интервале t1.
Иначе, отсутствие последствия означает независимость наступления событий во
времени.
3. Поток называется ординарным, если вероятность наступления двух и более
событий за некоторый достаточно малый интервал времени 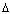
t пренебрежимо мала по сравнению с вероятностью наступления одного события за
этот интервал.
Поток, обладающий всеми тремя перечисленными свойствами называется простейшим.
47. Закон распределения числа событий за фиксированный промежуток времени и
закон распределения интервала времени между событиями в простейшем потоке.
Пусть рассматривается какой-то поток событий. С ним всегда можно связать
дискретную СВ – число событий, происходящих за интервал длины t. Эта СВ
дискретна. С этим же потоком можно связать НСВ – интервал времени между
событиями. Т – интервал времени между событиями в потоке. Для простейшего
потока доказано, что число событий, попадающих на интервал длины t является
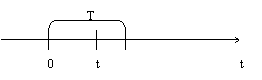
ДСВ, распределенной по закону Пуассона. Вероятность того, что за время t
произойдет ровно k событий.
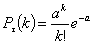 (a > 0) (a > 0)
a = t l, l - интенсивность простейшего потока
при t = 1
 Найдем закон распределения Найдем закон распределения
интервала времени между событиями простейшего потока. Выведем закон
распределения интервала времени между событиями в потоке.
F(t) = ?
Fт(t) = P(T<t) = 1 – P(T ³ t) = 1 – Pt(k=0) = 1 - 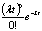 = 1 – e-lt, t ³ 0 = 1 – e-lt, t ³ 0
Fт(t) = le-lt
Всякий простейший поток можно задать интенсивностью, либо задать среднее
значение времени между событиями в потоке (Т).
Средняя продолжительность интервала времени 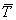 ; М(Т) = ; М(Т) = 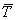 = = 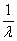 Þ l = Þ l = 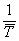
48. Многоканальная СМО с отказами.
СМО— система, предназначенная для обслуживания какого-то потока поступающих
на вход в систему заявок. Система характеризуется наличием того или иного числа
каналов обслуживания. Если в системе несколько каналов, то мы считаем эти
каналы равноправными, и они имеют одинаковые хар-ки (среднее число заявок,
обслуж. 1-им каналом при непрерывной работе за единицу времени—одно и то же для
всех каналов). Пусть СМО имеет n каналов обслуживания и на вход в систему
поступает простейший поток заявок с интенсивностью l. Будем считать, что
среднее время обслуживания одной заявки одним каналом Тоб=1/m; продолж. Обслуж.
Тоб—СВ, распределенная по показательному закону с параметром m. Тогда при
непрерывной работе канала он может обслужить m заявок в единицу времени
(технич., профес. Хар-ка каналов).
Пусть в случае, когда заявка, поступившая в систему, застает свободный хотя
бы один канал, то она поступает сразу под обслуживание каким-то одним
каналом. Если же заявка поступает в момент занятости всех каналов, то она
получает отказ в обслуживании и покидает систему необслуженной. Нарисуем граф
состояний таких СМО, при этом нумерацию состояний будем вести по числу
заявок, находящихся в системе: S0—заявок нет S1—одна заявка, один канал
занят, n-1 каналов свободно ,,, Sn—n заявок, n каналов занято, нет
свободных.
l l l l
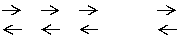
m 2m 3m (n-1)m nm
Вероятности состояний:
Р0=(1+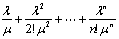 )-1 )-1
P1=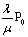 ; P2=(l2/(2!m2))*P0;....;Рr=(lk/k!mk)*P0 ; P2=(l2/(2!m2))*P0;....;Рr=(lk/k!mk)*P0
1. Ротказа=Рn ( все каналы заняты).
2. Относительная пропускная способность системы (вер-ть обслуживания)
q=1—Pотказа=1—Рn
3. Абсолютная пропускная способность(ср. число заявок, обслуж. за единицу
времени) A=lq
4. Среднее число занятых каналов 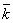 =Aq/m =Aq/m
Можно найти двумя способами:
5. кзан—число занятых каанлов—СВ . 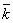 зан=М(кзан)= зан=М(кзан)=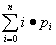
6.  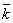
зан=A/m 5. 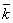
незан=n—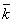 зан зан
7. Степень загруженности каналов s=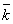
зан/n
49. Многоканальная СМО с ограниченным числом мест в очереди.
СМО— система, предназначенная для обслуживания какого-то потока поступающих
на вход в систему заявок. Система характеризуется наличием того или иного
числа каналов обслуживания. Если в системе несколько каналов, то мы считаем
эти каналы равноправными, и они имеют одинаковые хар-ки (среднее число
заявок, обслуж. 1-им каналом при непрерывной работе за единицу времени—одно и
то же для всех каналов). Пусть дана сис-ма с простейшим потоком, инт-ть
которого l, один канал в среднем может обслужить m заявок в единицу времени.
Пусть в сис-ме имеется m мест для постановки заявок в очередь. Предположим,
что заявка, заставшая в момент своего поступления один канал свободным, тут
же обслуж. Если же в момент поступления заявки все каналы заняты, но имеется
хотя бы одно свободное место в очереди, то заявка становится в очередь на
обслуживание, при этом как только один из каналов освобождается, одна заявка
из очереди поступает на обслуживание. Если заявка, поступившая в систему,
застает занятыми все каналы и места в очереди, то она получает отказ в
обслуживании и покидает систему. Возможные состояния системы: S0—заявок нет
S1—одна заявка, n-1 канал свободен, все места в очереди свободны Sn—n заявок,
все каналы заняты, все места в очереди свободны Sn+1—все каналы заняты, 1
заявка в очереди, m-1 мест в очереди свободны Sn+m—все каналы заняты, m мест
(все) в очереди заняты.
l l l l
l l
m 2m 3m nm
nm nm
Предельные вероятности состояний:
Р0=(1+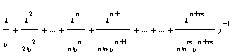
1.Ротказа=Рn+m=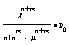 = =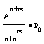
2.Относительная пропускная сп-ть q=1—Pn+m 3.Абсолютная пропускная сп-ть
A=lq 4.Среднее число заявок в очереди
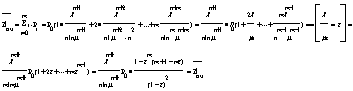
5. 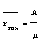 . 6. . 6. 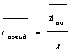
50. Многоканальная СМО с неограниченным числом мест в очереди.
51. Многоканальная СМО с отказами.
СМО— система, предназначенная для обслуживания какого-то потока поступающих
на вход в систему заявок. Система характеризуется наличием того или иного
числа каналов обслуживания.
Если в системе несколько каналов, то мы считаем эти каналы равноправными, и
они имеют одинаковые хар-ки (среднее число заявок, обслуж. 1-им каналом при
непрерывной работе за единицу времени—одно и то же для всех каналов).
Пусть число мест в очереди не ограничено. Хар-ки этой СМО получим из
характеристик СМО с ограниченным количеством мест в очереди, предполагая, что
m—>¥. Тогда в выражении для Р0 имеем
Р0=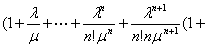 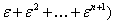 = =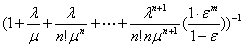
При m —>¥ å1+e+e2+...+em-1 сходится только в том случае, если
0<e<1; если e>=1 сумма расходится, т.е. для этой СМО процесс не
является транзитивным. Следовательно, предельные вер-ти состояний не
существенны.
Будем считать, что при m—>¥, e<1 . Следовательно предельн. вер-ти
сост-й сущ. и хар-ки СМО след.:
1. 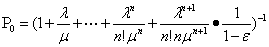
2. Ротказа=0
3. q=1 каждая заявка будет обслужена
4. 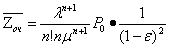 . .
5. Среднее время ожидания 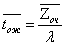 . 6.A=lq=l. 7. . 6.A=lq=l. 7.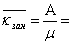 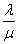
Страницы: 1, 2, 3, 4
| 


